Iglesia de Santa María de Bendones
Análisis compositivo
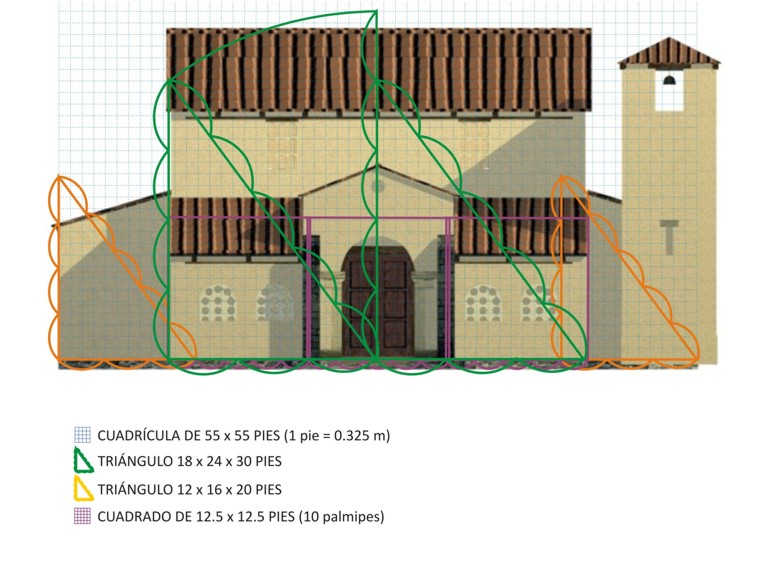
Partimos para este análisis de las respectivas plantas realizadas en su día por Joaquín Manzanares (Manzanares 1957), y Lorenzo Arias (Arias 2008), que hemos sometido a verificación compositivo-metrológica, determinando la presencia del conocido como «pie dórico» (1 pie = 0.324±0.326 m), estando todo el edificio inscrito en un cuadrado de 55 x 55 pies, convertibles a pasos (cuadrado de 11x11), o palmipes (cuadrado de 42x42, con 1 palmipes = 5 palmos).
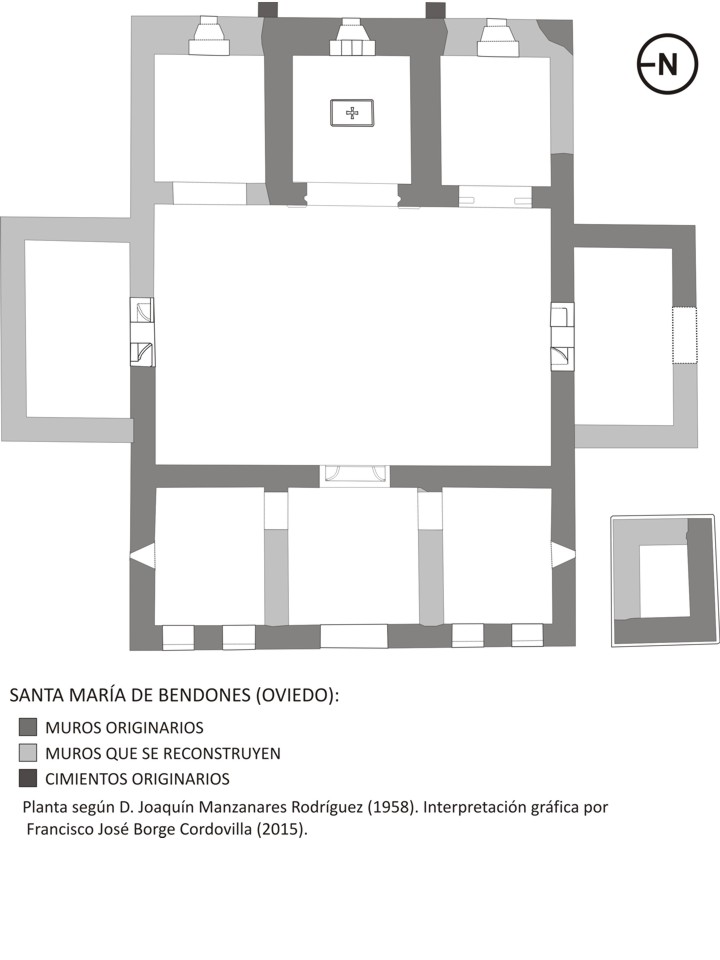

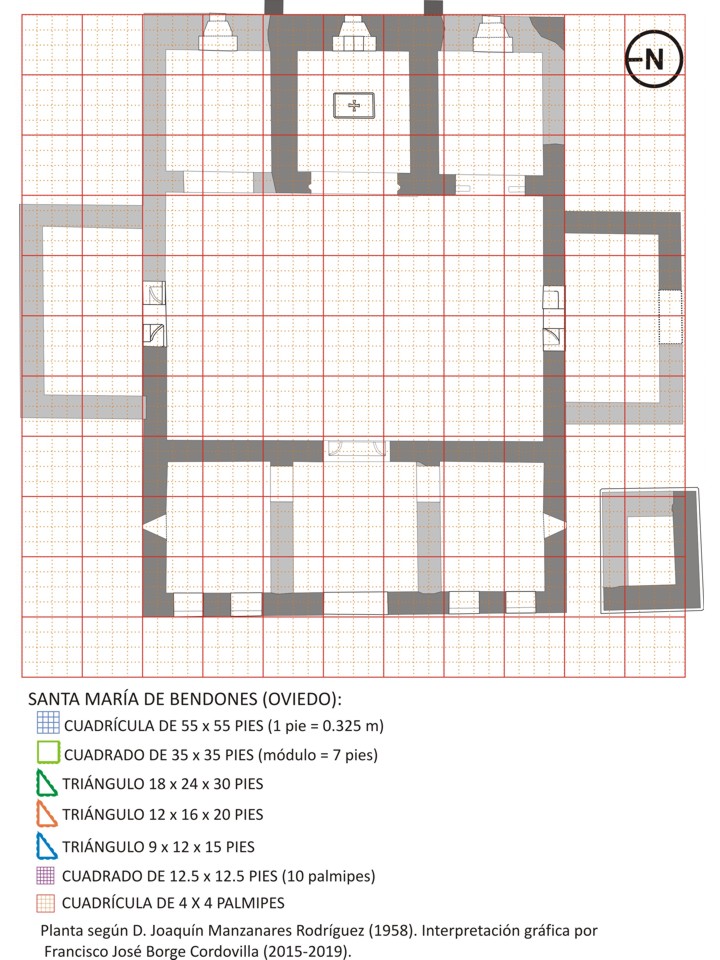
El sistema básico de trazado utilizado, al igual que en otros edificios religiosos analizados en los que, no obstante, la planta se articula de modo diferente, es la denominada proporción cierta, método de traza basado en las propiedades geométricas del cuadrado y la proyección de la diagonal del mismo. De este modo, la planta y sus subdivisiones básicas de articulación se trazan sobre un cuadrado de 35 x 35 pies, articulado en 5 módulos de 7 pies (1 módulo, 7 x 0.326 = 2.282 m). Mediante la proyección de la diagonal de dicho cuadrado se obtiene la aproximación geométrica del trazado completo del cuerpo central de la planta redondeándose, a efectos operativos, a un número exacto de 50 pies (la magnitud 35x√2, es un número inconmensurable, de valor 49.49 pies). El resultado de la aplicación del módulo antes definido a la planta geométricamente descrita, se obtiene la siguiente articulación básica de espacios, en sentido oeste -este: antecuerpo (pórticos), 2 módulos x 7 pies, total 14 pies; nave única, 3 módulos x 7 pies, total de 21 pies; cuerpo absidal, 2 módulos x 7 pies, total 21 pies..

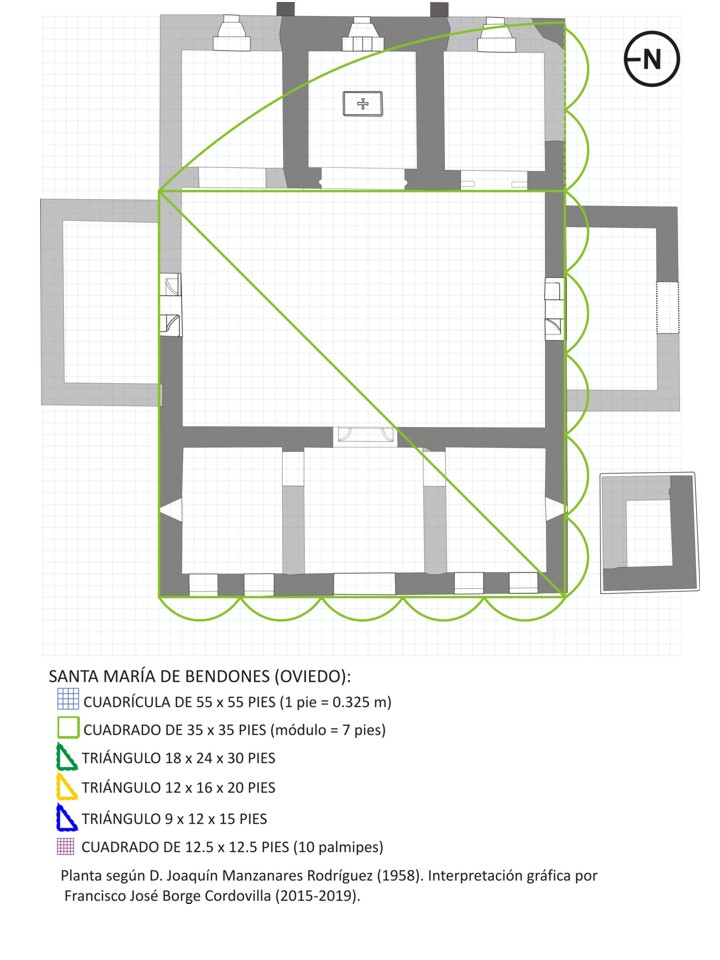
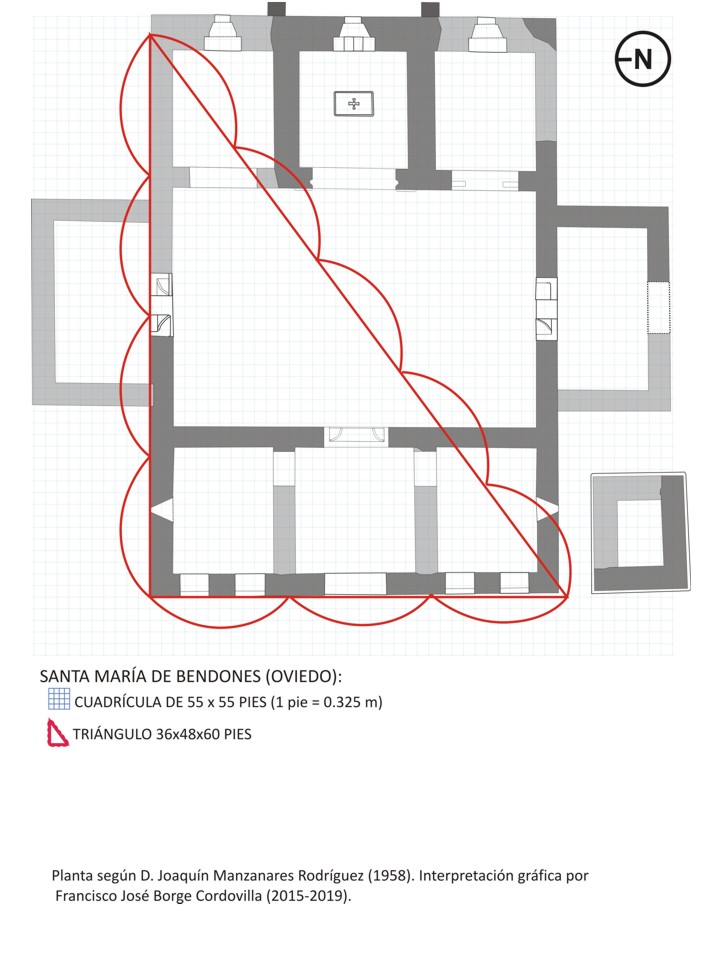
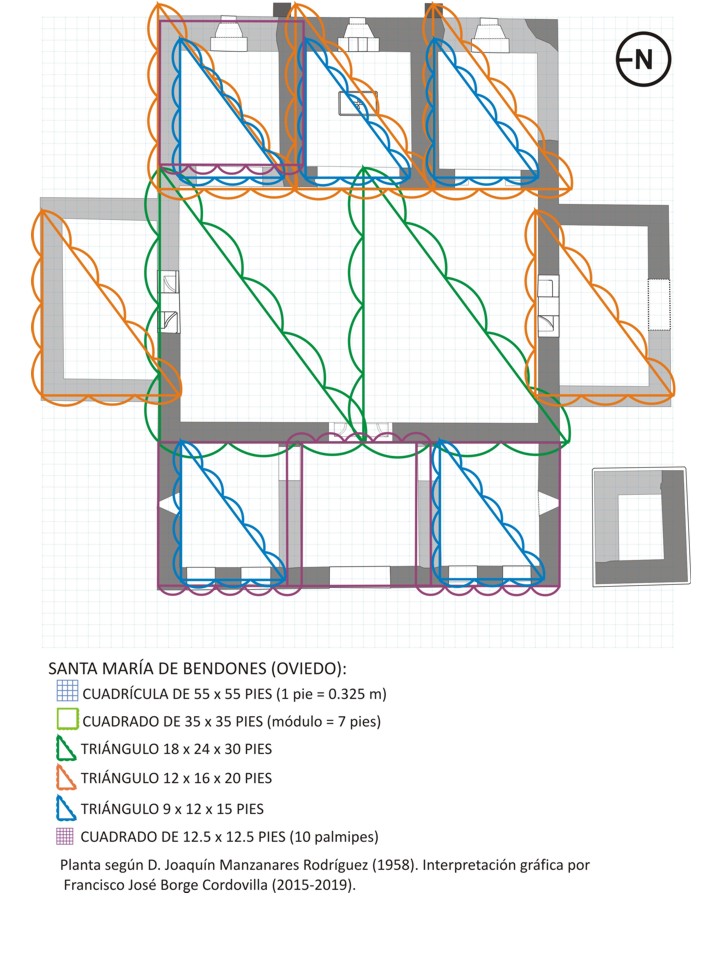
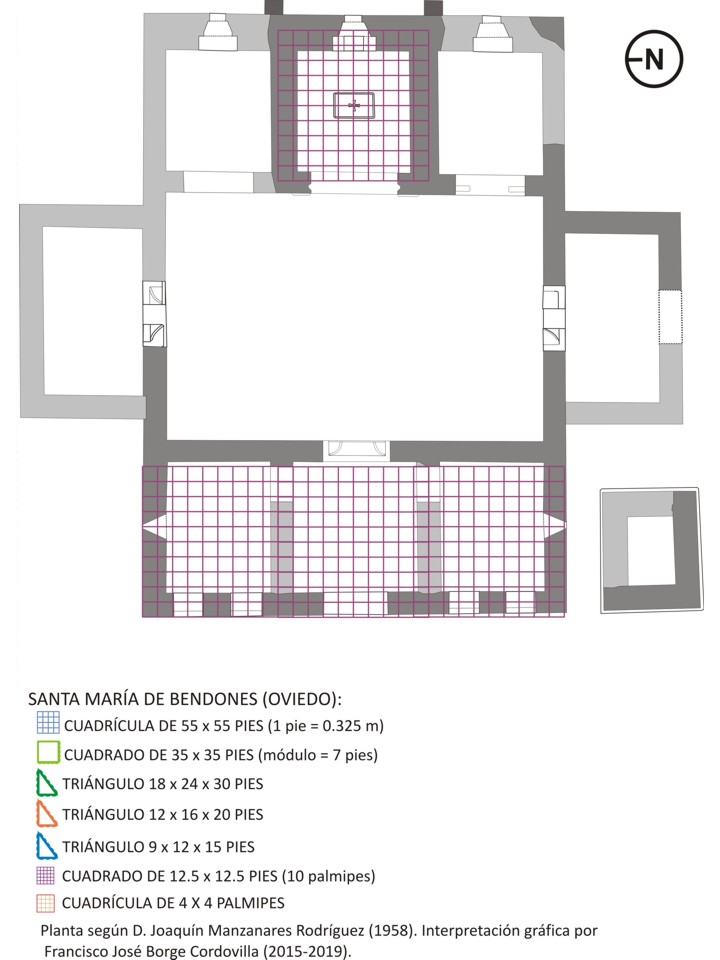
Para la articulación interior de los restantes elementos en planta, se recurrió a la triangulación de la misma, intercambiable, en algún caso, por la cuadrangulación. Así, la planta general que venimos de definir a través de la «proporción cierta», se puede aproximar igualmente aplicando la «proporción pitagórica», mediante un triángulo perfecto (proporciones 3-4-5) de 36 (cateto menor) x 48 (cateto mayor) x 60 (hipotenusa) pies, a partir de cuyos triángulos semejantes, submúltiplos del mismo, se obtienen las articulaciones de los espacios del templo, del siguiente modo: dos triángulos de 18x24x30 pies sirven para delimitar los planos exteriores de los respectivos muros este y oeste de la nave; triángulo de 12x16x20 pies, que determina las dimensiones de las respectivas habitaciones norte y sur, adosadas a la nave única; triángulos de 9x12x15 pies, que determinan el dimensionado interior de pórticos y ábsides. En este último caso, la división espacial entre pórticos y ábsides central y laterales, resulta igualmente interpretable a través de sendos cuadrados de 12,5 pies de lado, aunque, por redondeo de dimensiones, consideramos más probable la alternativa de la triangulación.
Para dimensionar los alzados, se utilizó igualmente la triangulación, proyectando el alzado los mismos triángulos utilizados para la definición de los respectivos cuerpos de edificio en planta: el triángulo de 18x24x30 pies, determina el alzado de la nave única, por proyección de su hipotenusa (30 pies), restando 3 pies (algo menos de 1 m) respecto a la rasante actual del tejado, afectada por la reconstrucción de la ruina, descubierta en la década de los años 50 del pasado siglo por D. Joaquín Manzanares, por parte del arquitecto D. Luis Menéndez Pidal Álvarez, a quien debemos el estado actual del edificio; el triángulo de 12x16x20 pies determina el alzado del pórtico central, por proyección en altura de su cateto mayor (16 pies), así como la altura de las respectivas habitaciones laterales adosadas a la nave, que es la longitud de su cateto menor (12 pies); por último la proyección en altura de la hipotenusa de este mismo triángulo perfecto determina el alzado total del ábside central (20 pies).
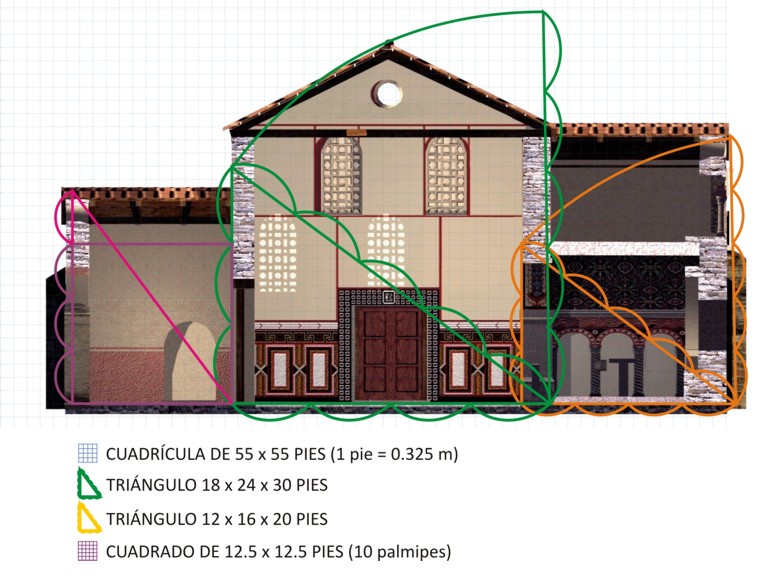
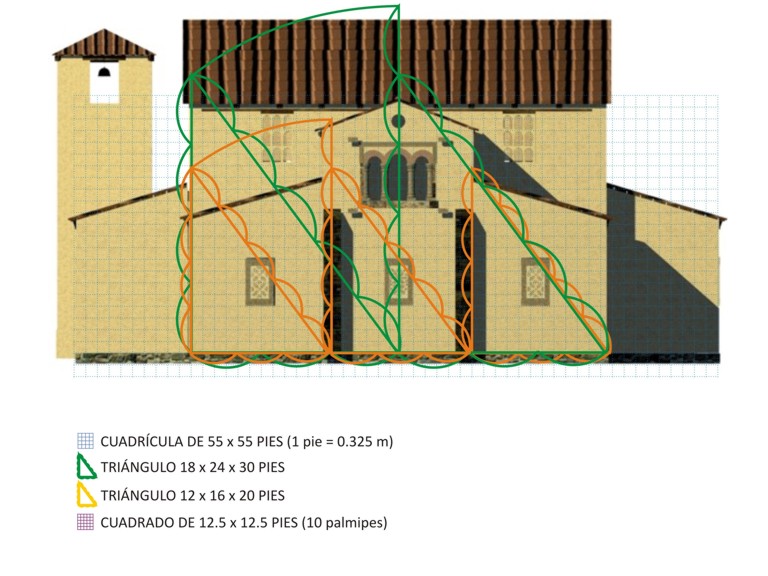
En cuanto a la articulación de las relaciones entre alzados de los diferentes cuerpos del edificio, éstas se articulan en base 2, siendo todas ellas múltiplos de 2 y conformando además una progresión aritmética de razón 2. Esto es: que cada una de las partes se relaciona en su alzado, con el volumen dominante de la nave única, según una progresión aritmética, de razón igual a 2 pies, de acuerdo a la serie numérica: 5 (ábside central - nave), 7 (ábsides laterales y pórtico central - nave), 8 (pórticos laterales y habitaciones laterales - nave).
Análisis metrológico
Del análisis metrológico del edificio se desprende, como hemos comentado, la presencia en el mismo del “pie dórico” de 0.326 m, y su múltiplo, el "palmipes" (pie de cinco palmos), tanto en la determinación de sus dimensiones globales, de 18 x 16.30 m (55 x 50 pies dóricos, o 44 x 40 palmipes), como de las particulares de cada uno de los principales espacios del edificio (ver figuras del análisis compositivo), donde puede constatarse la complejidad del diseño -a pesar de la simplicidad de la articulación de espacios- de este templo, y, a nivel metrológico, como, a partir del mencionado pie dórico, la articulación de los espacios del edificio puede explicarse mediante una cuadrícula de 4 palmipes, que se repite 11 veces en anchura por 10 veces en longitud, respecto a las medidas de los mismos en metros. Asimismo vuelve a constatarse la presencia de dimensiones convencionales, que no varían con independencia de la tipología del edificio, como es el ancho general de los muros (2 pies), y el de los muros de los santuarios, que se incrementa debido al abovedado de los mismos (3-4 pies).
Una vez más, del análisis compositivo-metrológico de este templo se pueden derivar conclusiones de alta probabilidad respecto a su cronología, ubicándolo dentro de la actividad del taller operante bajo Alfonso II (791-842),tanto por la presencia de la unidad de medida del "pie dórico", y su múltiplo el "palmipes", utilizado asimismo en el proyecto de la basílica de Santa María del Rey Casto ,como por la utilización en su proyecto y articulación de sus espacios de "triángulos perfectos" que se repiten en otros edificios del, presumiblemente, mismo taller: Santa María del Rey Casto, Santullano, San Tirso, San Pedro de Nora y la fuente de Foncalada.
Para ilustrar estos comentarios, presentamos el resumen del estudio metrológico en los siguientes cuadros:
| METROS | PASSVS | GRADVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|
| LONGITUD | 16,300 | 10,00 | 20,00 | 40,00 | 50,00 | 200,00 |
| ANCHURA | 11,440 | 7,018 | 14.037 | 28.074 | 35,092 | 140,368 |
| METROS | PASSVS | GRADVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|
| MÓDULO | 2,282 | 1,400 | 2,800 | 5,600 | 7,00 | 28,00 |
| 1/2 MÓDULO | 1,141 | 0,700 | 1,400 | 2,800 | 3,500 | 14,00 |
| 1/7 MÓDULO | 0,326 | 0,200 | 0,400 | 0,800 | 1,00 | 4,00 |
| METROS | MÓDULO | 1/2 MÓD. | 1/7 MÓD. | PASSVS | GRADVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|---|---|
| ÁBSIDES | 4,238 | 1,857 | 3,714 | 13,00 | 2,600 | 5,200 | 10,400 | 13,00 | 52,00 |
| NAVE ÚNICA | 7,824 | 3,429 | 6,857 | 24,00 | 4,800 | 9,600 | 19,200 | 24,00 | 96,00 |
| PÓRTICO | 4,075 | 1,786 | 3,571 | 12,500 | 2,500 | 5,00 | 10,00 | 12,500 | 50,00 |
| METROS | MÓDULO | 1/2 MÓD. | 1/7 MÓD. | PASSVS | GRADVS | PALMIPES | PES | PALMVS | |
|---|---|---|---|---|---|---|---|---|---|
| NAVE ÚNICA | 11,410 | 5,000 | 10,00 | 35,00 | 7,00 | 14,00 | 28,00 | 35,00 | 140,00 | ABSIDE CENTRAL | 4,401 | 1,929 | 3,857 | 13,500 | 2,700 | 5,400 | 10,800 | 13,500 | 54,00 |
| ABSIDE LATERAL | 3,586 | 1,571 | 3,153 | 11,00 | 2,200 | 4,400 | 8,800 | 11,00 | 44,00 |
| PÓRTICO CENTRAL | 4,564 | 2,00 | 4,00 | 14,00 | 2,800 | 5,600 | 11,200 | 14,00 | 56,00 |
| PÓRTICO LATERAL | 3,423 | 1,500 | 3,00 | 10,500 | 2,100 | 4,200 | 8,400 | 10,500 | 42,00 |
| MEDIDA | EQUIVALENCIAS | En m | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DECEMPEDA | 1 | 3,260 | |||||||
| PASSVS | 2 | 1 | 1,630 | ||||||
| GRADVS | 4 | 2 | 1 | 0,815 | |||||
| CVBITVS | 6,67 | 3,34 | 1,67 | 1 | 0,489 | ||||
| PALMIPES | 8 | 4 | 2 | 1,2 | 1 | 0,408 | |||
| PES | 10 | 5 | 2,5 | 1,5 | 1,25 | 1 | 0,326 | ||
| SEMIS | 20 | 10 | 5 | 3 | 2,5 | 2 | 1 | 0,163 | |
| PALMVS | 40 | 20 | 10 | 6 | 5 | 4 | 2 | 1 | 0,082 |